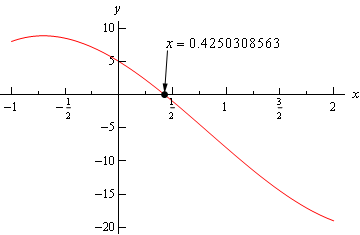BQ #7: Unit V- Difference Quotient

The Difference Quotient is something we've become very familiar with this year. But what we might not know is what it means and where is it derived from. Simply enough, the difference quotient formula is just the slope formula mixed around, more specifically the slope of all tangent lines.

http://cis.stvincent.edu/carlsond/ma109/diffquot.html

 

 

The slope formula is what? (y2-y1)/(x2-x1). If we refer to the points of f(x+h), F(x), and such, "h" representing the distance between the first point and the second. Our ordered pairs will be seen as (x, f(x)) and (x+h, f(x+h)). By plugging in both ordered pairs to the formula, the result would be f(x+h)-f(x)/x+h-x. When we cancel the x's we would get: f(x+h)-f(x)/h and VOILA the difference quotient!

BQ #6: Unit U

1. What is a continuity? What is a discontinuity?

Up to this point, we've all become familiar with continuities. A continuity can be described or classified by many different aspects, one being it is predictable. By the graph being predictable, we always know where its headed on either sides because it continues on forever and ever. Because the function reaches infinity on both sides, we must know why; because it has no jumps, no breaks, and no holes. Why? Because it's continuous! A break is when the graph stops at a simple value, a jump os when the graph breaks into two separately placed functions that land on different left and rights; a hole is the lack of a value. These all three entail that at some point, the function stops which means it is no longer continuous. A continuity can be drawn without ever lifting a pencil.

http://faculty.wlc.edu/buelow/calc/nt2-4.html

2. What is a limit? When does it exist? What is the difference between a limit and a value?

To start, a limit is an indented height of a function. A function has many, many limits because they can be found basically anywhere on the graph. However, this does not mean that EVERY function has a limit, no because there are several types of functions. As we've gone over the difference between continuities and discontinuities, we know that discontinuities are grouoed into two categories: removable (a point discontinuity where the function has a limit but also has the value in a different y-value) and un-removable(a jump where they have different left and right positions, an oscilating which means it has no set x-value, and an infinite which is classified by an asymptote that causes unbounded behavior).

http://en.wikipedia.org/wiki/Classification_of_discontinuities

 This example shows two different un-removable discontinuities, an oscillating and an infinite. Because the oscilatiing entails that there is no set value, then we know that the limit does not exist. Same goes for the infinite; because it reaches towards infintity by the vertical asymptote, the value is virtually never reached because infinity is not a true value. This means that the value is never reached ergo the limit does not exist.

http://en.wikipedia.org/wiki/Classification_of_discontinuities

There is one more where the limit does not exist; in jump functions. A limit is where both the left and the right mesh to the same place when going towards the center. In a jump, we cannot trace to the same position by the left and right so we say that it has different left-and-right. Ultimately, this means that the limit does not exist.

From this, we can assume that limits do not exist in unremovable discontinuities. The same cannot be said for removable which is a point discontinuity. If we refer to the picture above again and avoid one of the functions, we will see that it has one function with a hole and a strange dot that signifies the actual value. This is a point discontinuity where the limit and value both exist which means that the limit also exists.

3. How do we evaluate limits?

When we evaluate limits numerically, we basically put them in a table. This table is used to show where the function goes when approaching a value.

x	-5.1	-5.01	-5.001	-5.0001	-5	-4.9999	-4.999	-4.99	-4.9
g(x)	23.2	23.1	23.001	23.0001	24	249999.9	24999.9	249.9	24.9

http://people.hofstra.edu/stefan_waner/realworld/tutorials/frames2_6a.html


Usually, this is done by moving by a tenth each time. as seen in the photo above, we see that the graph gradually gets closer and closer to the value in the middle.

When we evaluate limits graphically, we do just that! By graphing the function.

http://people.hofstra.edu/stefan_waner/realworld/tutorials/frames2_6b.html

 

To evaluate graphically just means that we need to graph the function and see the graph and the way it actually looks. This generally is better way of evaluating because we can see the values and limits all in one photo.

 

Algebraicallly, a limit can be evaluated one of three ways: through substitution, factoring, and rationalizing.

10. https://www.youtube.com/watch?v=CvB4080WC48
Although we always want to start with direct substitution. This means that we substitute the number being approached for every x value. If the value is 0/0 then we have to change methods. The factoring method is next because it allows us to cancel out to then simplify. If neither work, we refer to rationalzing and multiplying with conjugates. Usually this allows us to break it down into an easier solution. Then after conjugating we once again directly substitute for all the x variables.

BQ #4: Unit T Concept 3

Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill? Use unit circle ratios to explain.
We know that the ratio for tangents are y/x which is sine/cosine. We also know that sine and cosine have all values so if cosine were to be zero than that would make the ration undefined! Hmm, what was that thing about undefined again? OH, right! Undefined means there is an asymptote! Here is where we look at the graph and decide where tangent will be negative or positive. According to the unit circle, we already know that tangent is positive in the first quadrant which but negative in the second! SO when looking at a graph, we see the tangent line high above the x-axis in range of 0 to pi/2 but as soon as we go pi/2 to pi, what happens? it becomes negative and goes downhill but because it starts off as negative (by the asymptote) and then reverses to positive, a tangent graph is normally uphill!. This is because it is just another presentation of the Unit circle!
Cotangent is much like its reciprocal but has its own qualifications. Its ratio is x/y- or cosine/sine. To find our asymptotes now we want SINE to be equal to zero. According to the Unit Circle sine has asymptotes at zero and pi! Then we continue with the same steps as for tangent and decide in which quadrants is cotangent positive and negative in: positive in one and three but negative in two and four! The Asymptote really gives us where the graph really begins. And because we can see that the cotangent graph starts out as a positive above the x-axis but then transcends into the negative, it is called a downhill! 

(Mrs. K's unit T: Exploration Packet)

BQ #3: Unit T Concept 1-3

How do graphs of sine and cosine relate to the others? Emphasize asymptotes.
For the rest of our lives we are going to refer to sine and cosine as being our "favorite cousins." Why, you might ask? Because they relate to our other trig functions through their ratios! By knowing this we already know that they will have some grand effect on the other four trigs.

Tangent
We know that Tangent's ratio is... y/x! Which, when referring to the unit circle values (sin = y/1 & cos = x/1), is equivalent to Sin/Cos. If we imagine the unit circle being unfolded to lay as the graph, we can picture the four sections that represent four quadrants; at the same time, we would place both sine ans cosine in the graph segment as well.  The area between zero and pi/2 would be known as Quadrant one. if we focus specifically on where sine and cosine are, we see that both are abooooove the x-axis! Therefore, because of tangents ratio, we know that tangent is also positive n the first quadrant. Curious about where the we get the placements of the asymptotes? Easy! Where there is an undefined value, there is an asymptote and we'd only get undefined by dividing by ZERO! Ergo, asymptotes will be wherever cosine is at zero.

Cotangent
Cotangent is very similar to tangent because they are what? Reciprocals! This means that the ratio for cotangent would be x/y because sine is the value of y and cosine the value of x. Again, we know that cosine, sine, and cotangent will intersect on the graph because of that one ratio. Now, we have to figure out the asymptotes. Because y is the denominator, we noe have to figure out where sine is at zero because it would create an undefined value therefore an asymptote! The only places where y equals zero is at (1,0) and (-1,0). Here, the radians are at zero and pi.

Secant
Secant is a little more different than tangent and cotangent because its period does not end at pi, but at two-pi which makes a complete revolution. Secants ratio is 1/cos. Although it takes longer, we can tell the positive or negative sign through the same method. If cosine is positive then of course secant will be positive as well! Our asymptotes for secant will always be the same as the asymptotes for tangent because they both have cosine as their denominator! However, because secant only has cosine in its ratio, instead of having a normal curve for tangent, their graph becomes a parabola facing the direction of positive or negative, depending on the quadrant.

Cosecant
With cosecant, we are going to see very similar things as we did with secant. The only difference is the value in its ratio. the ration for Cosecant is 1/sine. This means that the asymptotes for cosecant and cotangent will be equivalent because they too have the same denominator. When drawing a cosecant or secant graph, we always start with drawing its reciprocal FIRST because it is the general foundation of this graph, After drawing the reciprocal, we draw the asymptotes. For cosecant our asymptotes will be wherever sine is zero! From there, we draw the parabolas starting at the maximums and minimums of each hill on the reciprocal.

BQ #5: Unit T Concept 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

 We can explain why sine and cosine do not have asymptotes simply by referring to their trig ratios: sin= y/r & cos= x/r. Because we are using the Unit Circle, the radius will always be the absolute value of one. If the radius will always be one then we know that the ration will never be undefined because the value cannot be zero. Now here is where we can see the connection: if there is no undefined value, automatically we know that there are no asymptotes.
This cannot be applied to their reciprocals nor tangent or cotangent because these trig function rations can have any value as the denominator which includes zero that would make it undefined. This is because both the y and the x values have no restrictions.  

BQ #2: Unit T Concept Intro

How do trig graphs relate to the Unit Circle?
Ultimately, we can say that a trig graph, in its first period, is just a different presentational form of the Unit Circle that has been unwrapped on a graph. In referring to the original form of the Unit Circle, we know that each trig function has two quadrants where they are positive and two where they are negative. For example, sin is positive in both the first and second quadrants but negative in the third and fourth. By knowing that they are positive in the first and second, we know that the distance from the beginning of Quad 1 and Quad 2 is 0 to pi; the distance from Quad3 to Quad 4 is 3pi/2 to 2pi where we know sine is negative. What a trig graph generally represents is the sign change for all trig function values by stating if the values are positive (above the x-axis) and if they are negative (below the x-axis). This forms wave like motions on the graph.

 

The trig graphs will go on forever repeating the same period for each trig function.

 



Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?
Sine and Cosine both have a period that end at 2pii because that is when the pattern ends. A period is the end to a pattern on the graph. Because Tangent has a pattern of positive-negative in the first two quadrants and repeats for the third and fourth, we know that the period for tangent and cotangent are cut down to half which is just pi.

How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?
So why is it that sine and cosine have an amplitude of one? Maybe the Unit Circle can answer that. When we look at the trig functions sin = y/r and cos = x/r; because it is the unit circle, we automatically know that r is the value of one. So it is because we may only divide by one that we must assume that the move must be a value of one or negative one. This also explains why the trig of sin and cosine may not equal any value that does not lie between one and negative one. However, these do not apply to any other function. Why not, you ask? Well let's look at tangent; the ration for tangent is y/x. There are no restriction values for either y or x which means that there is a possibility for the number to exceed the distance of one in either direction. the same applies for the other trigs.

Reflection #1 - Unit Q: Verifying Trig Identities

1. Reflect on your learning this unit, specifically with concept 1 and 5.

Although this Unit made me pull my hair out, I did learn much more about trig functions! :)
  1. What does it actually mean to verify a trig identity?
Well, my dear, all it means is just that: to verify the answer. When verifying, you are given an "equation" that has two separate portions equal to each other. To "solve" we would have to prove how the problem on the left can equal what is on the other side. But there is one thing to always remember: never touch the right side! In other words we cannot do anything such as divide, multiply, square or square-root because those would have to apply to BOTH sides which we cannot do of course!
  2. What tips and tricks have you found helpful?
It is always better to right your identities on a flashcard and memoriiiiiiiiiiiiiiiiize  all of them! This will cut the time of having to keep referring to the beginning of your packet and just make these stubborn trig functions easier in general. Also, practice-practice-and-more-practice! You might feel comfortable with a few problems but just remember that there are so many different ways an equation can be set up that we want to be as familiar as we can with any method.
  3. Explain your thought process and steps you take in verifying a trig function.
When verifying, i always want to see if i can change them all to functions of sin and cosine simply because they're easier to work with. If we are given fractions, most of the time it would be helpful to also separate in portions to cancel and/or substitute with better identities. Also remember that our main focus is to get the same answer as on the right without ever ever EVER E-V-E-R touching it! Just keep practicing and it'll come to you eventually.